불 함수 개념 이해
디지털 기기는 모두 이진 정보를 저장하고 처리하도록 설계된 칩을 탑재하는데, 이 칩들은 모양이 다르더라도 기초 논리게이트라는 동일한 구성 블록으로 만들어진다.
이번 1장에서는 Nand를 통해서 논리 게이트를 만든다.(Not, And, Or, Xor, 멀티플렉서, 디멀티플렉서)
불 대수(Boolean Algebra)
불 대수는 1/0, true/false와 같은 이진값을 다룬다.
불 함수는 이진수를 입력받아서 이진수를 출력하는 함수이다.
불 연산자(Boolean Operator)
불 연산자는 일반적인 세 가지 불 함수를 의미하는데, 각각 And, Or, Not이다.
"·", "+" , overbar로 나타내거나 "∧", "∨", "¬"로 나타낸다.
아래 이미지는 연산자를 확인하기 위해 가져온 이미지이다. +는 or 연산, · 은 and 연산, not은 overbar로 나타난다.
아래와 같지 않더라도 x and y를 x ∧ y로 나타낼 수도 있다. (명제의 논리 연산자)
쉽게 생각해서 True/False 값을 가지는 p와 q로 표현하던 고등학교 수학의 명제를 생각해도 될 것 같다.

출처: https://monkey-engineer.tistory.com/8
세 가지 기본 불 함수에 대해서 진리표를 한 번 만들어보자.
| x | y | x and y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| x | y | x or y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| x | not x |
|---|---|
| 0 | 1 |
| 1 | 0 |
이 외에도 여러 불 함수들이 존재한다.
책에 나와있는 변수가 두 개일 때 표현할 수 있는 불 함수 표를 작성하면 다음과 같다.
| 불 함수 표현식 | x = 0 | x = 0 | x = 1 | x = 1 |
|---|---|---|---|---|
| y = 0 | y = 1 | y = 0 | y = 1 | |
| constant 0 | 0 | 0 | 0 | 0 |
| x And y | 0 | 0 | 0 | 1 |
| x And not y | 0 | 0 | 1 | 0 |
| x | 0 | 0 | 1 | 1 |
| not x and y | 0 | 1 | 0 | 0 |
| y | 0 | 1 | 0 | 1 |
| x Xor y | 0 | 1 | 1 | 0 |
| x Or y | 0 | 1 | 1 | 1 |
| x Nor y | 1 | 0 | 0 | 0 |
| Equivalence | 1 | 0 | 0 | 1 |
| Not y | 1 | 0 | 1 | 0 |
| If y then x | 1 | 0 | 1 | 1 |
| Not x | 1 | 1 | 0 | 0 |
| If x then y | 1 | 1 | 0 | 1 |
| x Nand y | 1 | 1 | 1 | 0 |
| Constant 1 | 1 | 1 | 1 | 1 |
두 이진 변수에 대한 모든 불 함수를 표현한 것이다. 일반적으로 n개의 2진 변수에 대한 불 함수의 개수는 2^(2^n) 개이다.(그래서 n이 2인 지금은 16개의 함수가 작성되어 있다.)
각 연산자는 연산의 의미를 묘사하는 일반적인 이름이 나와있다.
예를들어 Nand는 Not(And(x,y))인 Not-And를 줄인것이다. Xor은 Exclusive Or을 줄인 것으로 두 개의 변수 중 하나만 1일 때 1이 된다.
위의 표에서 재밌는 점을 찾아보면 모든 연산은 And, Or, Not으로 표현할 수 있다. (논리적인 표현식을 적기에는 너무 귀찮아서 안 적었는데, x+y와 같은 표현식으로 확인하면 더 직관적으로 알 수 있다.)
And, Or, Not 연산은 또 다시 Nand로 표현할 수 있다. 여기서 우리가 생각할 수 있는 건 Nand 연산만 있으면 모든 연산을 할 수 있다는 점이다.
불 함수
모든 불 함수는 두 가지 방식으로 정의할 수 있다.
하나는 진리표, 다른 하나는 표현식이다.
진리표는 모든 가능한 값들을 찾아서 정리해놓은 것을 말하고, 표현식은 (x Or y) And (Not z)와 같은 식을 말한다.
진리표와 불 표현식
변수 n개의 불 함수가 불 표현식으로 표현되면 항상 진리표를 구성할 수 있으며, 그 역도 성립한다.
컴퓨터 구현에 있어서 진리표와 불 표현식, 표현식을 다른 방식으로 구성해내는 것 등은 중요하다.
진리표는 세상의 상태를 기술하고, 표현식은 그 상태를 실리콘에 구현하는 것을 편리하게 만들어준다.
그리고 하나의 표현식을 다른 표현으로 수정하는 것은 하드웨어 설계에서 매우 중요하다. 예를 들어, (x Or y) And (Not x Or y)라는 식이 있다고 생각해보자.
이 식은 다른 방식으로 표현하면 y다. 이처럼 복잡한 식을 단순화하여 하드웨어에 대한 최적화를 이룰 수 있다.
진리표와 불 표현식에 대한 설명
정확히는 증명이라고 되어 있는데, 이 증명 이라는 단어가 나에게 큰 혼동을 주었다.
책의 증명은 수학적인 엄밀한 증명이라기 보다는 예시를 통해서 할 수 있다~ 정도로만 설명해주고 있다. 만약 엄밀한 수학적 증명에 대한 관심이 있다면 논리학 혹은 이산수학 교재에서 찾아보자.
앞서서 불 함수가 불 표현식으로 표현되면 항상 진리표를 구성할 수 있고, 그 역도 성립한다고 했다.책에서는 진리표로 불 표현식을 도출해내는 과정을 설명해준다.
진리표에서 불 표현식을 도출하기 위해서 우리는 다음과 같은 단계를 따를 수 있다.
- 출력이 1인 모든 입력 조합을 확인한다.
- 각 입력 조합마다 그 조합에서만 1이 되는 표현식을 만든다.
- 이 표현식을 모두 OR로 연결한다.
예를들어, XOR 함수의 진리표를 확인해보자.
x y | x XOR y
0 0 | 0
0 1 | 1
1 0 | 1
1 1 | 0출력이 1인 입력 조합은 (0, 1), (1, 0)이다.
- (0, 1)에서만 1이 되는 표현식: (Not x) And y
- (1, 0)에서만 1이 되는 표현식: x And (Not y)
전체 표현식은 ((Not x) And y) Or (x And (Not y))가 된다.
불 표현식을 줄이는 방법
고등학교에서 배웠던 교환 법칙, 결합 법칙, 분배 법칙, 드 모르간의 법칙, 멱등 법칙이 모두 기억이 나는가?
이 법칙들은 불 대수에서도 적용이 되고, 활용해서 표현식을 줄일 수도 있다.
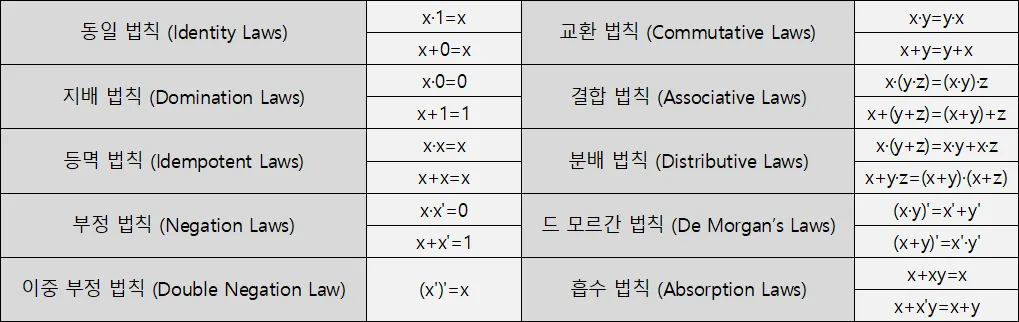
출처: https://homubee.tistory.com/31
단어 정리
- 진리표
- 모든 명제 및 그 조합의 불 함수에 대한 입출력 결과를 기록한 표
참고
https://ko.wikipedia.org/wiki/%EB%B6%88_%EB%8C%80%EC%88%98
https://en.wikipedia.org/wiki/Boolean_expression
'개발 > 개발 공부' 카테고리의 다른 글
| [밑바닥부터] 3일차 - 1장 불 논리: 프로젝트 (0) | 2025.04.07 |
|---|---|
| [밑바닥부터] 2일차 - 1장 불 논리: 논리 게이트와 HDL 소개 (1) | 2025.04.07 |
| 밑바닥부터 만드는 컴퓨팅 시스템으로 학습하기 (0) | 2025.04.04 |
| OAuth 2.0에 대해 알아보기 (0) | 2025.03.15 |
| [WebSocket과 Socket.io] 1편 - WebSocket (0) | 2025.01.16 |


